Quick Primer on Metric Spaces
Table of Contents
Vector Space
A vector space is set of mathemetical objects that can be multiplied and added together to produce objects of the same kind. This notion of vector spaces proves to be a very useful framework for extending methods and structures to very different types of problems. A few special types of vector spaces you may be already be familiar with:
Function Spaces
We can add functions together and scale them as well.
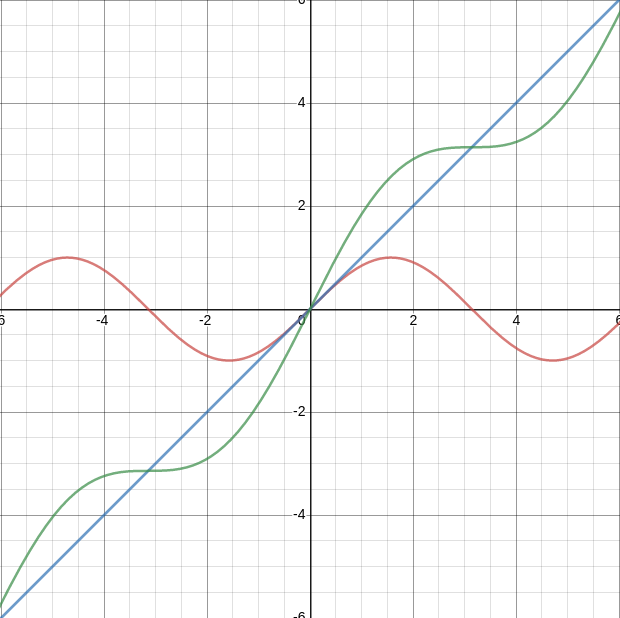
Figure 1: Additive Property of Functions
In Figure 1 we can see there exists:
- A function in blue \(f(x) = x\)
- A function in red \(g(x) = \sin(x)\)
Taking the summation of these two functions produces a third function in green \((f + g)(x) = \sin(x) + x \)
Euclidean Spaces
We can add \(i, j, k\) together and scale them as well to produce a vector \(a\) .
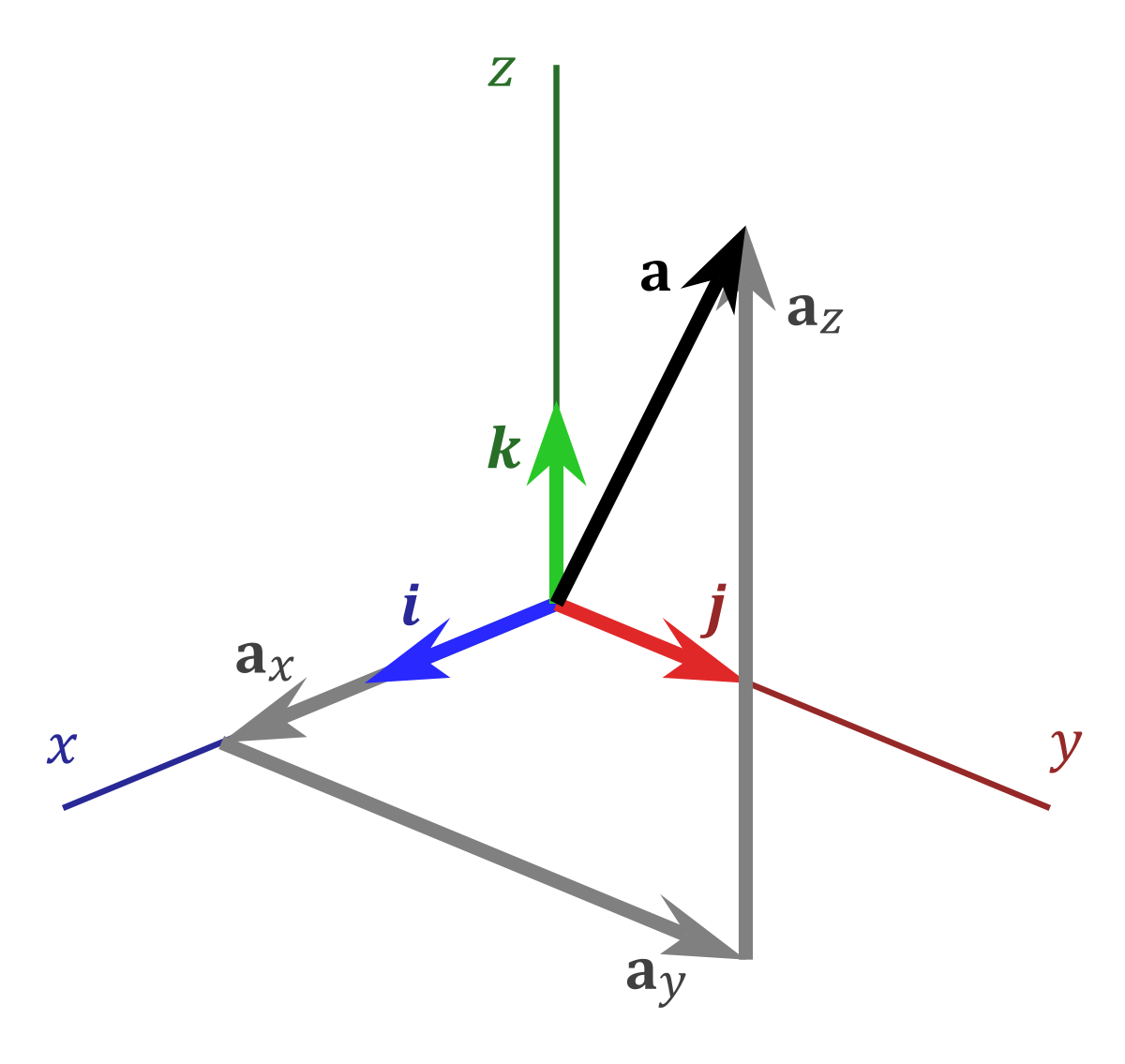
Figure 2: Vector Space Visualized.
Typically this is the vector space you learn in linear algebra because it is intuitive to understand and very helpful for extending additional structure into spaces.
More Formally
Definition: A field is a set \(\mathbb{F}\) of numbers, such that \(a, b \in \mathbb{F} \implies a+ b, a - b, ab, \frac{a}{b} \in \mathbb{F}.\) Some examples of sets that would count as fields are the real numbers \(\mathbb{R}\) and the complex numbers \(\mathbb{C}\) .
Definition: A Vector Space consists of a set \(\textbf{V}\) , a field \(\mathbb{F}\) and two operations:
- Vector Addition: \(\textbf{a}, \textbf{b} \in \textbf{V} \implies \textbf{a} + \textbf{b} \in \textbf{V}\)
- Scalar Multiplication: \(c \in \mathbb{F}, \textbf{v} \in \textbf{V} \implies c\textbf{v} \in \textbf{V}\)
Metric Space
Essentially a metric is a measurement to see how similar two vectors are to one another. In geometrical terms, this similarity could be interpreted as distance.
Definition: A Metric Space consists of a set \(\textbf{V}\) , and has a notion of distance \(d(x,y) \ \forall x, y \in \textbf{V}\) . That is \(d : \textbf{V} \times \textbf{V} \to [0;\infty)\) and satisfies these following properties \(\forall x,y,z \in \textbf{V}\) :
- Identification: \(d(x,y) = 0 \implies x = y\)
- Symmetry: \(d(x,y) = d(y,x)\)
- Triangle Inequality: \(d(x,y) \leq d(x,z) + d(z,y)\)
As long as these axioms hold true for a particular vector space with a function d, then it can be categorized as a metric space. A few examples you may be familiar with are the euclidean distance metric, or L2.